有序数组的平方

给你一个按 非递减顺序 排序的整数数组 nums，返回 每个数字的平方 组成的新数组，要求也按 非递减顺序 排序。

 

示例 1：

输入：nums = [-4,-1,0,3,10]
输出：[0,1,9,16,100]
解释：平方后，数组变为 [16,1,0,9,100]
排序后，数组变为 [0,1,9,16,100]
示例 2：

输入：nums = [-7,-3,2,3,11]
输出：[4,9,9,49,121]
 

提示：

1 <= nums.length <= 104
-104 <= nums[i] <= 104
nums 已按 非递减顺序 排序
 

进阶：

请你设计时间复杂度为 O(n) 的算法解决本问题

1. 对于一个存在负数的升序数组而言,平方后升序无非就是对每一个元素的绝对值大小进行比较

2. 所以最大的值一般存在于数组的头和尾,我们使用两个指针依次进行比较即可完成O(n)排序

class Solution {
public:
    vector<int> sortedSquares(const vector<int>& nums) {
        //两侧数大于中间的原因可以从0点看 去比较两侧数的绝对值大小 abs(-2) > abs(1)
		//所以我们可以从两侧开始比较依次放入数组即可
        int i = 0;
		int j = nums.size() - 1;
		int count = 1;
		vector<int> result = nums;
        for (;i<=j;)
        {
            if (nums[i] * nums[i] >= nums[j] * nums[j]) {
                result[result.size()-count] = nums[i] * nums[i];
				i++;
				count++;
            }
            else if (nums[i] * nums[i] < nums[j] * nums[j]) {
				result[result.size() - count] = nums[j] * nums[j];
				count++;
                j--;
            }
        }
        return result;
    }
};

给定一个含有 n 个正整数的数组和一个正整数 target 。

找出该数组中满足其总和大于等于 target 的长度最小的 子数组 [numsl, numsl+1, ..., numsr-1, numsr] ，并返回其长度。如果不存在符合条件的子数组，返回 0 。

示例 1：

输入：target = 7, nums = [2,3,1,2,4,3]
输出：2
解释：子数组 [4,3] 是该条件下的长度最小的子数组。

示例 2：

输入：target = 4, nums = [1,4,4]
输出：1

示例 3：

输入：target = 11, nums = [1,1,1,1,1,1,1,1]
输出：0

提示：

• 1 <= target <= 109

• 1 <= nums.length <= 105

• 1 <= nums[i] <= 104

进阶：

• 如果你已经实现 O(n) 时间复杂度的解法, 请尝试设计一个 O(n log(n)) 时间复杂度的解法。

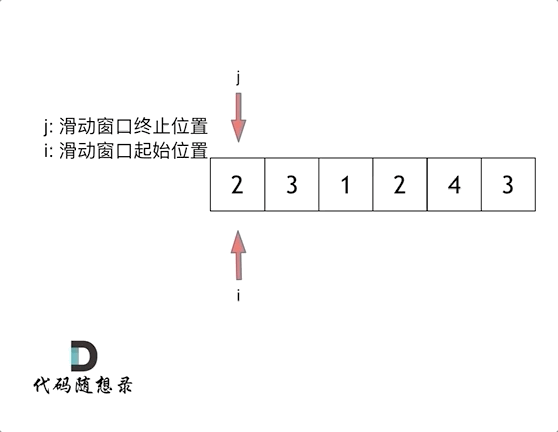
class Solution {
public:
    int minSubArrayLen(int target, vector<int>& nums) {
		int minLength = nums.size() + 1; // 初始化为数组长度+1
		int sum = 0; // 当前子数组的和
        //i左指针 指向起始点
        int i = 0;
		//j右指针 指向结束点
        for (int j = 0; j < nums.size(); j++)
        {
			sum += nums[j]; // 将当前元素加入到和中
            // 当当前和大于等于目标值时，尝试缩小左边界
            while(sum>=target)
            {
				minLength = min(minLength, j - i + 1); // 更新最小长度
				sum -= nums[i++]; // 减去左指针指向的元素 i++是为了缩小窗口并且移动左侧起始指针
            }
        }
		// 如果没有找到符合条件的子数组，返回0
		return minLength == nums.size() + 1 ? 0 : minLength; // 如果没有找到符合条件的子数组，返回0
    }
};